Технологии квантовых компьютеров в 2022: достижения, ограничения

За последние полвека индустрия информационных технологий прочно закрепилась в нашей жизни и сформировала чёткий образ того, насколько компьютеры могут быть эффективны. Для огромного количества задач известны оптимальные алгоритмы решения, практически полностью реализующие потенциал современных вычислителей. Но возможно ли решать эти задачи ещё быстрее? Как преодолеть теоретические барьеры математики? Возможный ответ — поменять правила игры.

Совершенно не обязательно, что если что-то невозможно выполнить на классическом компьютере, то это невозможно сделать в принципе. Просто необходимо использовать другой подход к концепции самих вычислений и алгоритмов, при котором математические ограничения, доказано распространяющиеся на привычные нам компьютеры, оказываются неприменимы. Одним из наиболее перспективных вариантов такого альтернативного подхода являются квантовые вычисления.

Концепция квантового компьютера, появившись в 80-х годах прошлого века, к сегодняшнему дню успела развиться до уровня строгого математического формализма, воплотиться в металле и даже постепенно начать входить в нашу жизнь. Ведь в области квантовых технологий по меньшей мере лежит и щит, и меч информационной безопасности – квантовые компьютеры представляют потенциальную угрозу, а для защиты от них применяются методы квантовой и пост-квантовой криптографии, уже достаточно широко представленные на рынке.

Изначально было ясно, что многие квантовые алгоритмы не имеют прямых классических аналогов. Например, ускоренный поиск по неструктурированной базе данных, работающий быстрее последовательного перебора, или телепортация квантовой информации – перенос квантовых данных между двумя носителями таким образом, что физически между ними передаётся только информация классическая. Дело в том, что квантовые компьютеры остаются в определённом смысле аналоговыми, и такие сугубо квантовые алгоритмы не вписываются в парадигму детерминированных цифровых классических вычислений. По этой же причине многие из квантовых алгоритмов кажутся совершенно контринтуитивными и не вписываются в наши привычные представления. Долгое время оставался открытым вопрос, существует ли задача, в которой квантовые компьютеры будут обладать доказуемым качественным преимуществом по сравнению с классическими. Данный вопрос получил название задачи поиска квантового превосходства. Значительный шаг вперёд в этом направлении был осуществлён только в 2019 году, когда исследователи Google AI Quantum экспериментально продемонстрировали, как квантовый компьютер справляется с задачей, на решение которой у классического вычислителя, по представлениям исследователей, ушло бы несколько десятков тысяч лет [1]. И хотя данное исследование содержит только неподкреплённую строгим математическим доказательством практическую демонстрацию, а его результаты впоследствии вызвали в научных кругах широкую дискуссию с вескими аргументами за обе стороны вопроса, можно полагать, что в данный момент мы находимся на заре эпохи практического квантового превосходства. Безусловно, это оказывает значительное влияние на индустрию информационных технологий в целом, и, в частности, на её экономику. Всё больше мировых IT-гигантов, таких как IBM, Google, Microsoft, Amazon и Alibaba вкладывают огромные ресурсы в разработку квантовых вычислителей и исследование квантовых алгоритмов. Несмотря на то что квантовые компьютеры пока остаются довольно слабыми и едва ли могут незамедлительно перевернуть все рынки, множество мировых экспертов сходятся во мнении, что компетенции в области квантовых вычислений могут стать одним из ключевых аспектов эффективного развития информационно-технологической экосистемы уже в ближайшем будущем.

Рост индустрии

После демонстрации квантового превосходства исследователями Google, индустрия квантовых вычислений начала привлекать всё больше и больше внимания. Заинтересованы данной областью как исследователи, так и инвесторы [2]. Это вполне объяснимо — мир едва начал свыкаться с экономическими и индустриальными последствиями революции, порождённой взрывным развитием технологий классических компьютеров. И тут на горизонте возникает новая область – квантовые вычисления, которая, кажется, имеет все шансы на повторение такого поразительного взлёта. Сообщение о способности квантового компьютера на практике решать задачу, принципиально неподвластную классическому вычислителю, для многих стало сигналом о том, что компьютеры нового типа неизбежно достигнут нужного уровня совершенства и займут свою нишу уже в ближайшем будущем. Ещё больше подогрели интерес к ситуации сами исследователи Google, заявив, что по аналогии с законом Мура для классических компьютеров, можно ожидать роста характеристик квантовых вычислителей с экспоненциальной скоростью [1]. Оглашение подобной перспективы мгновенно привело к взрывному росту числа тематических публикаций, регистрируемых патентов, а также компаний-стартапов в области квантовых вычислений [3].

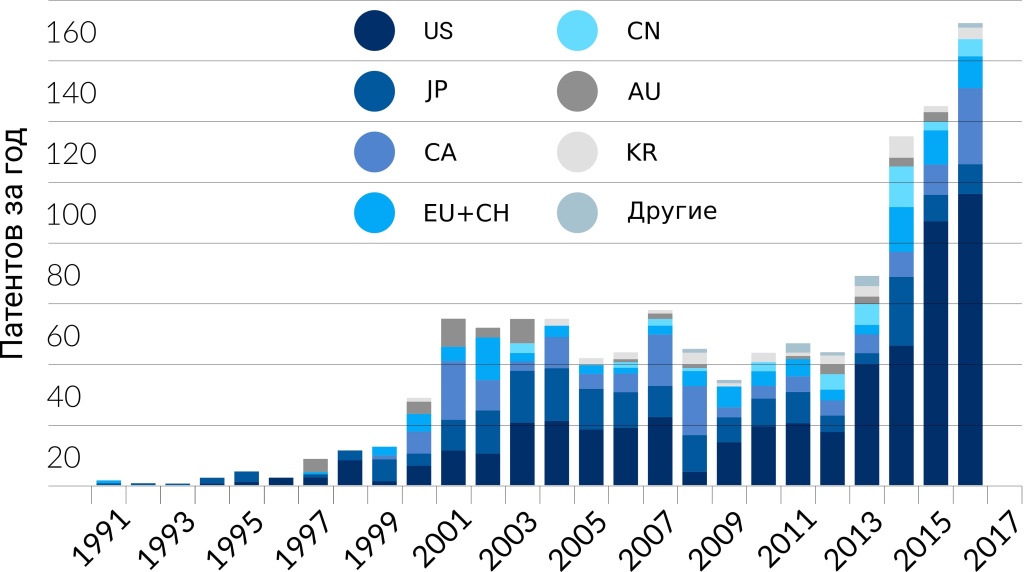
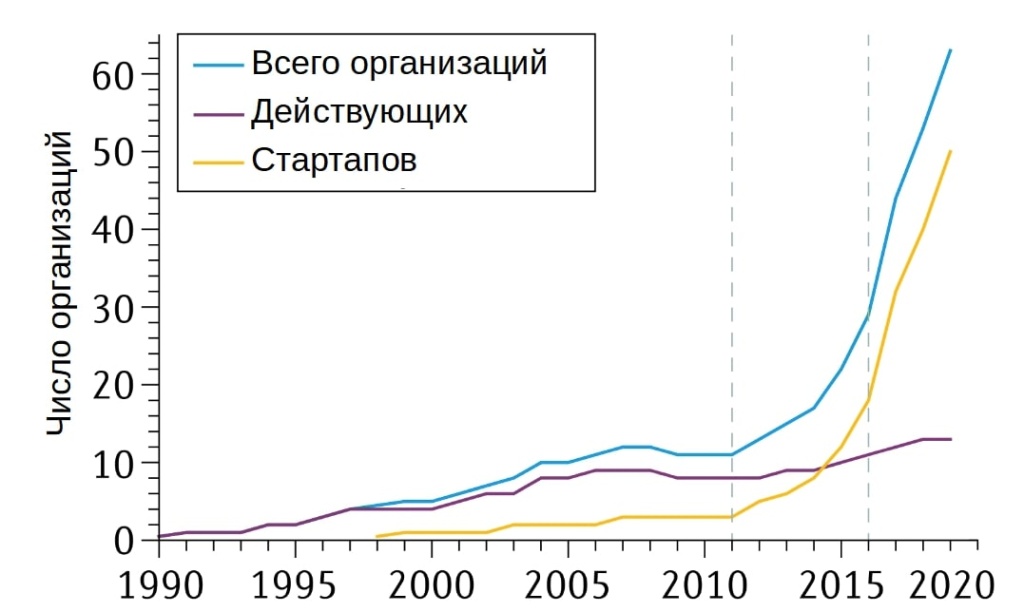
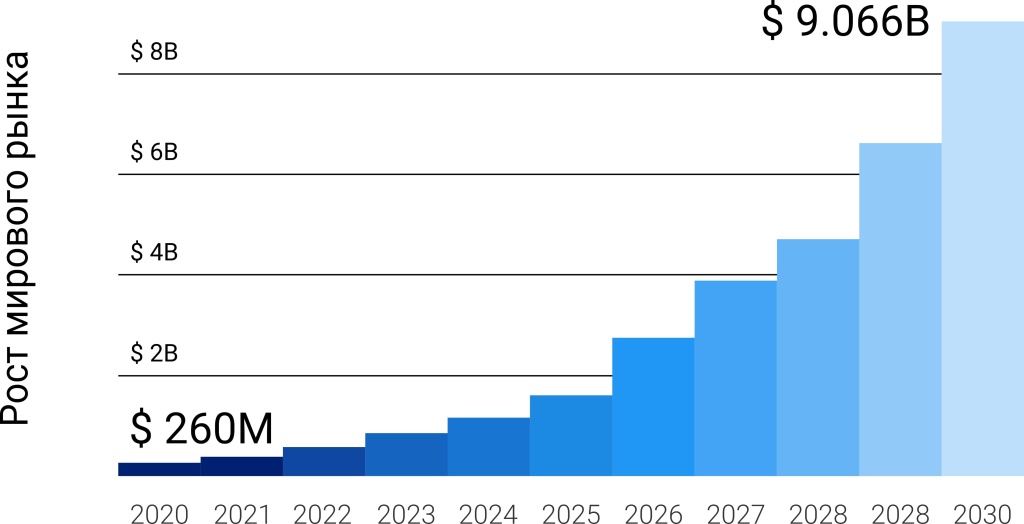
С другой стороны, если разобраться в ситуации более детально, то окажется, что создание масштабируемого квантового вычислителя сопряжено с рядом технологических сложностей. Тезис демонстрации квантового превосходства в значительной мере подвергается критике. Задача, на которой он был продемонстрирован, в реальности бесполезна, а временные рамки обещаний практически значимого квантового вычислителя постоянно сдвигаются [5 ; 6; 7]. В этом, безусловно, есть доля истины. Но настолько ли далека перспектива распространения квантовых вычислителей, чтобы можно было обходить их вниманием?

Цель данной статьи – сформировать у читателя понимание возможных сценариев развития квантовых компьютеров, их потенциального места среди других существующих технологий, а также текущего прогресса в борьбе с практическими ограничениями, препятствующими широкому распространению продуктов и сервисов на основе квантовых вычислений уже сегодня.

Парадигма квантовых вычислений

Прежде всего определим, какое место квантовые вычислители могут в перспективе занять в устоявшейся индустрии информационных технологий.

Как известно, классические компьютеры оперируют битами — единицами информации, которые позволяют различить два состояния системы: 0 и 1. В основе логики квантового компьютера лежит схожее понятие – кубит. Кубит — объём информации, описывающий квантовую систему с двумя состояниями. В отличие от бита, кубит может принимать промежуточные значения, сочетающие вклад состояний 1 и 0 в разных пропорциях. Например, возможно состояние 50/50 или 70/30. Если кубита два, то возможных вкладов в состояние становится четыре: 00, 01, 10, 11. И так далее в геометрической прогрессии. Если число кубитов приближается к нескольким сотням, то памяти всех классических компьютеров не хватит, чтобы сохранить полный объём информации о состоянии такого регистра.

На практике это в совокупности с особенностями обработки и считывания квантовой информации приводит к тому, что отдельные задачи на квантовом вычислителе начинают решаться качественно быстрее, чем на классическом. Например квантовый алгоритм Шора позволяет разложить число на простые множители с экспоненциальным ускорением [8], а алгоритм Гровера – осуществить поиск по неструктурированной базе данных с квадратичным ускорением [9]. Из первого следует потенциальное разрушение криптографической стойкости шифров с открытым ключом на основе RSA, а из второго – квадратичное ускорение решения любой NP-задачи и соответствующее снижение стойкости симметричных шифров. То есть для обеспечения того же уровня секретности понадобится вдвое более длинный ключ.

Математически доказано, что квантовый компьютер способен эффективно моделировать классический [10]. То есть всё, на что способен классический компьютер, квантовый компьютер способен исполнить по крайней мере не хуже. Однако на практике квантовый компьютер сегодня – весьма сложная лабораторная установка, отдельные элементы которой зачастую требуют криогенного охлаждения. Главным ограничением квантового компьютера является ограничение по объёму обрабатываемых данных. В лучшем случае сегодня это несколько сотен кубитов, что никак нельзя сравнить с доступными классическим вычислителям гигабайтами оперативной памяти. Поэтому реальный сценарий использования квантового вычислителя — гибридный. Вся инфраструктура остаётся классической, и только при необходимости произведения отдельных специфичных расчётов классическая программа удалённо подключается к квантовому вычислителю, передаёт ему данные и считывает результат.

Единственная технология, которая остаётся за рамками такой картины – квантовые коммуникации. Квантовая криптография, которая как раз способна обеспечить концептуальную защиту от атаки квантовым вычислителем, требует создания новой инфраструктуры для передачи квантовой информации. Это может быть оптическое волокно или атмосферный лазерный канал. Не исключается использование на оптическом канале дронов и спутников.

Также, помимо непосредственно программируемых квантовых компьютеров, возможно использование проблемно-специфичных квантовых устройств. С их помощью, например, на линиях квантовых коммуникаций может осуществляться коррекция ошибки без считывания квантового состояния. Данный тип устройств не предъявляет больших требований по числу кубитов или объёму исполняемой программы и теоретически может быть реализован на имеющейся сегодня технологической базе.

Из всего перечисленного выше формируется образ перспективной информационной инфраструктуры. Квантовые вычислители не повлияют существенным образом на облик имеющихся сегодня сервисов, оставив все конечные пользовательские интерфейсы привычно классическими. Может повыситься скорость обработки данных в отдельных задачах за счёт доступа пользовательских устройств к облачным квантово-вычислительным сервисам. Также появится квантовая информационная инфраструктура, в первую очередь для квантовой криптографии. Это будут стационарные, либо мобильные, но маловероятно, что карманные устройства для квантового распределения ключей. Вполне возможно, что более простые и компактные по сравнению с полноценными компьютерами квантовые вычислительные системы будут использоваться на конечных пользовательских узлах для обработки квантовой информации.

Квантовые алгоритмы и возможности квантовых вычислителей

Ступень развития, на которой сегодня находятся квантовые вычислители, получила название NISQ – Noisy Intermediate-Scale Quantum – квантовые устройства среднего масштаба без коррекции ошибок. Название отражает две главные проблемы, сдерживающие развитие квантовых компьютеров – сложность создания регистра большого объёма и большая подверженность влиянию внешних шумов. Две этих проблемы неразрывно связаны. То, что под влиянием шума квантовые состояния со временем теряют заложенную в них информацию, влияет на нашу способность контролировать одновременно большое число кубитов.

Экспериментальные реализации квантовых вычислителей только чуть более года назад перешагнули рубеж в 100 кубитов в регистре [11]. Теоретически, этого уже достаточно, для экспериментальной реализации некоторых алгоритмов криптоанализа. Реализация атаки Гровера на алгоритм Simplified-AES требует всего 32 кубита [12]. Атака полноценного AES-128 может быть выполнена при 384 доступных кубитах [13]. Однако глубина данного алгоритма такова, что к концу его исполнения полезная информация в вычислительном регистре будет почти полностью уничтожена шумами.

Справиться с такими нежелательными эффектами призвана технология коррекции ошибок. Вероятность того, что несколько кубитов одновременно потеряют информацию о своём состоянии под действием шумов – ниже, чем для одного. Для коррекции ошибок вводится понятие логического кубита, состояние которого кодируется несколькими физическими кубитами. Если часть физических кубитов, кодирующих один логический, оказалась зашумлена, их состояния могут быть восстановлены с опорой на информацию, сохранённую в остальных кубитах. Таким образом, для повреждения состояния логического кубита необходимо, чтобы к моменту выполнения коррекции большая доля физических кубитов была значительно зашумлена.

Такой подход в теории позволяет бороться с шумами, но кратно увеличивает требования к объёму регистра квантовых вычислителей. Объём регистра, необходимого для выполнения атаки Гровреа на AES с применением коррекции ошибок составляет от нескольких тысяч до десятков тысяч кубитов. Объём регистра, необходимого для атаки шифра RSA алгоритмом Шора преодолевает порог в сто тысяч кубитов. Возможность реализации вычислителя с регистром такого объёма в ближайшие пять лет представляется крайне маловероятной. Однако не исключено, что первые попытки лабораторной реализации подобных алгоритмов или их элементов начнут появляться к концу десятилетия. 

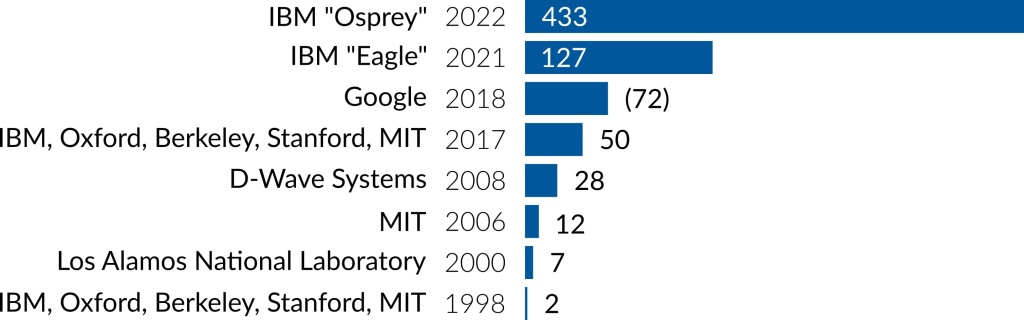
Другим возможным подходом к борьбе с шумами является не коррекция, а подавление ошибок [14]. Наиболее распространёнными являются подходы с так называемой экстраполяцией к нулевому шуму и с применением в схеме дополнительных параметризованных гейтов, призванных статистически подавлять влияние специфических шумов. Преимуществом подхода является то, что он не требует увеличения числа физических кубитов в алгоритме.

Метод экстраполяции к нулевому шуму является наиболее простым методом подавления ошибки, и он отлично подходит для применения в вариационных квантовых алгоритмах. Данный тип алгоритмов — самый реальный кандидат на практическое использование в NISQ-устройствах. Вариационный алгоритм сочетает использование квантового вычислителя для ускоренного расчёта некоторой целевой функции с использованием классического оптимизатора. Можно сказать, что прямая реализация принципа, высказанного Ричардом Фейнманом: для расчёта состояний квантово-механической системы используется квантовый вычислитель. В зависимости от того, какая квантовая схема используется, оптимизируемая целевая функция может решать задачи квантовой химии, оптимизации или даже криптоанализа [15, 16]. Интереснее всего то, что неизвестны точные асимптотики эффективности квантовых вариационных алгоритмов. В отдельных случаях они способны демонстрировать результаты, превосходящие и классический оптимизатор, и даже квантовый алгоритм Гровера. В совокупности со сравнительно низкими требованиями по числу кубитов вариационные алгоритмы можно оценить как потенциально одну из самых близких к практическому внедрению технологию из области квантовых вычислений.

Сверхпроводники

Долгое время квантовые компьютеры на основе сверхпроводящих кубитов удерживали рекорд по доступному объёму вычислительного регистра. Именно на машине такой архитектуры было продемонстрировано практическое квантовое превосходство [1]. В основе физической реализации данного типа кубитов лежит квантование уровней энергии электрического колебательного контура в условиях сверхпроводимости. Такой подход обеспечивает достаточно высокую степень точности исполнения операций, однако поддержание вычислителя в сверхпроводящем состоянии требует создания криогенных температур в значительном объёме. Это, в свою очередь, ведёт к существенной чувствительности вычислителей данного типа к внешнему воздействию, а также создаёт дополнительные препятствия для масштабирования.

Тем не менее, достижением 2022 года является представленный компанией IBM вычислитель Osprey с 433 сверхпроводящими кубитами [17]. Если представленный годом ранее Eagle, обладающий 127 кубитами, теоретически позволял промоделировать отдельные элементы атаки S-AES с простейшей коррекцией ошибок, например, с девятикубитным кодом Шора, то в регистре Osprey можно проводить эксперименты со значительно более сложными и совершенными кодами коррекции. В контексте этого вызывает интерес исследование методов подавления ошибки на уровне логических кубитов. Точная оценка перспектив этих подходов требует более подробных экспериментальных данных, однако, можно утверждать, что IBM пока достаточно успешно поддерживают тренд роста числа кубитов сверхпроводниковых вычислителей.  Озвученным прогнозом специалистов IBM стало получение компьютера с 4000 кубитов к 2025 году. И, несмотря на всю кажущуюся амбициозность данного заявления, фундаментальных ограничений, которые могли бы препятствовать достижению заявленных параметров, нет. Если специалисты IBM справятся с подавлением шумов и поддержанием когерентности для регистра с таким количеством кубитов – они смогут выполнить обещание.

Холодные атомы

Вычислители на основе холодных атомов не требуют криогенного охлаждения кубитов. Теоретически, за счёт возможности наращивания числа оптических ловушек, удерживающих атомы, и большей устойчивости к шумам, вычислители данного типа обладают несколько большим потенциалом масштабирования, по сравнению с квантовыми компьютерами на основе сверхпроводящих цепей. В то же время возникающие при работе с атомными кубитами ошибки в значительной мере поддаются контролю за счёт методов подавления. Это было продемонстрировано в 2021 году с представлением программируемого атомного симулятора на 256 кубитов [18].

По количеству кубитов для архитектуры на основе холодных атомов рекорд прошлого года – 256 кубитов на программируемом симуляторе, остаётся актуален. Однако произошел прорыв в технологии реализации двухкубитных гейтов. Поскольку атомы электрически нейтральны, они не взаимодействуют на расстоянии. Реализация двухкубитного гейта для них требует возбуждения одного из атомов в состояние с очень высокой энергией, называемое ридберговским. В таком состоянии радиус, на котором атомы могут взаимодействовать, существенно увеличивается и наблюдается эффект ридберговской блокады: если один атом уже находится в ридберговском состоянии, это приводит к смещению электронных уровней соседнего атома, что не позволяет возбудить его в ридберговское состояние при помощи характерного лазерного импульса. На основе этого эффекта может быть построен запутывающий гейт [19].

Новый подход использует ультракороткие лазерные импульсы для одновременного возбуждения атомов в ридберговские состояния за пределами режима ридберговской блокады [20]. Это даёт возможность преодолеть характерное временное ограничение и перейти от микросекундного временного масштаба к наносекундному. И, хотя рекордная точность операции пока не продемонстрирована, такой подход за счёт скорости взаимодействия атомов ведёт к значительному снижению вероятности возникновения ошибки при применении двухкубитного гейта.

Новый тип запутывающих гейтов не предоставляет технологию для реализации квантовых операций с гигагерцовой частотой. Однако он позволяет преодолеть характерный временной барьер, так что вычислитель, построенный на гейтах такого типа, теоретически сможет по порядку величины приблизиться к быстродействию классических компьютеров.  В совокупности со сравнительно долгим временем жизни атомного кубита данная технология в перспективе существенно повышает потенциал масштабируемости вычислителей на основе холодных атомов.

Оптические кубиты 

Электрическая нейтральность атомов обеспечивает им меньшую чувствительность к шумам окружающей среды, но, в то же время, создаёт сложности для обеспечения взаимодействия атомов между собой. Это заставляет использовать более сложные схемы реализации двухкубитных гейтов, такие как гейты на основе ридберговской блокады. Ещё дальше в этом направлении заходят кубиты на основе фотонов. Фотоны практически не взаимодействуют ни с окружением, ни между собой. За счёт этого они, с одной стороны, практически не подвержены влиянию шума, но, с другой, реализация запутывающего гейта для фотонных кубитов в ряде случаев связана с фундаментальными ограничениями. По этой причине до недавнего времени оптические квантовые вычислители оценивались как наиболее перспективные на временном горизонте от 10 лет. Но в 2021-2022 годах стали доступны новые технические возможности, позволяющие обойти характерные для оптической архитектуры фундаментальные ограничения.

Существуют несколько способов кодирования кубита в состоянии фотона. Наиболее простые – поляризационный кубит и двухрельсовая кодировка. Поляризационный кубит подразумевает сопоставление состояний 1 и 0 ортогональным поляризациям, например, вертикальной и горизонтальной. Двухрельсовая кодировка предлагает кодировать один кубит в паре оптических мод, сопоставленных состояниям 0 и 1, в одной из которых находится фотон. В обоих случаях из-за слабого взаимодействия фотонов реализация двухкубитного гейта требует использования нелинейной среды. Причём величина нелинейности должна на много порядков превосходить достижимые значения.

Ввиду технической невозможности прямой реализации был найден альтернативный подход, названный протоколом KLM (Knill, Laflamme, Milburn) [21]. Он позволяет реализовывать двухкубитный запутывающий гейт с использованием только линейных элементов, однако получаемая схема имеет ограниченную вероятность успешного срабатывания. Такой подход уже является приемлемым для экспериментальных задач, и позволяет реализовывать квантовые вариационные алгоритмы с малым числом кубитов. Однако конечная вероятность успешного срабатывания гейта ведёт к экспоненциально малой вероятности срабатывания всей схемы при её масштабировании, что недопустимо.

Преодоление этого ограничения потребовало выработки ещё одного альтернативного подхода. Из характеристик квантового состояния светового пучка могут быть выделены отдельные параметры, связанные соотношением неопределённостей Гейзенберга. Связь данных параметров позволяет кодировать в них состояние кубита. В некотором смысле это подобно тому, как оно кодируется в поляризации. Получаемый кубит называется кубитом на сжатых состояниях, поскольку для кодирования информации одна из квадратур сжимается сильнее стандартного квантового предела.

Оказывается, что кубиты на сжатых состояниях можно телепортировать с использованием базовых оптических элементов. А корректируя протокол телепортации, можно менять телепортируемое состояние [22]. В обычных условиях такое изменение является нежелательным, но при работе со сжатыми состояниями скорректированную телепортацию можно использовать для реализации гейта. Телепортируя многокубитные состояния, можно реализовать многокубитные гейты детерменированным образом. Необходимо только владеть технологией приготовления запутанных состояний высокой размерности, необходимых для осуществления телепортации. Но опять же, для сжатых состояний генерация запутанности возможна при помощи базовых оптических элементов. Экспериментально была продемонстрирована генерация запутанных кластерных состояний на данной архитектуре объёмом до 1000000 кубитов.

Строго говоря, сжатые состояния не являются кубитами. Кубит является лишь подмножеством пространства сжатых состояний. И телепортационные гейты не обеспечивают возможности произвольной трансформации сжатого состояния. Однако если специально выделить из сжатого состояния кубит, то и это ограничение удаётся преодолеть. Более того, оставшиеся степени свободы сжатого состояния можно использовать для дублирования состояний кубита, и таким образом реализовывать коррекцию ошибки.

На подобную реализацию рассчитан код коррекции Готтесмана-Китаева-Прескилла (GKP) [23]. Он обеспечивает устойчивую коррекцию ошибок, если степень сжатия состояния, то есть отношение дисперсии квадратур, достигает 15-17дБ, а в теории — 10дБ [24]. Экспериментальные же результаты сегодня демонстрируют техническую возможность достижения сжатия состояния до 15 дБ, чего может быть достаточно для экспериментальной демонстрации коррекции ошибки.

Таким образом для оптической архитектуры удалось преодолеть фундаментальные ограничения реализации запутывающего гейта, технически показана возможность создания регистра до 1000000 кубитов, архитектура включает естественный механизм коррекции ошибки, а продемонстрированный уровень шумов находится на границе устойчивой коррекции. Безусловно, все эти результаты были продемонстрированы в независимых экспериментах, опубликованные значения являются пиковыми и разработка единого вычислителя, использующего все представленные технологии, представляет собой сложнейшую инженерную задачу. Но необходимо констатировать, что имеющиеся результаты позволяют перевести оптическую архитектуру из ранга потенциально перспективного кандидата для реализации масштабируемого квантового вычислителя на дальних временных горизонтах в ранг актуального игрока. Это демонстрирует канадская компания Xanadu, 1 июня 2022 года представившая в публичном доступе вычислитель на сжатых состояниях с регистром из 216 оптических мод [26].

Заключение

С учётом всего вышеизложенного, можно вернуться к представлению об интеграции квантовых вычислений в индустрию информационных технологий.

Отрасль в целом демонстрирует ожидаемый планомерный рост, сопряженный с последовательным решением инженерных задач. Это отражается в появлении квантовых вычислителей с большими чем раньше объёмами квантовых вычислительных регистров.

Доминирующей архитектурой остаются кубиты на основе сверхпроводников. Однако малое время жизни кубитов данного типа, связанное с их большой чувствительностью к шумам и необходимостью криогенного охлаждения, ставит под вопрос величину нереализованного потенциала масштабируемости данной технологии. Можно ожидать, что в ближайшие 3-5 лет технология будет оставаться основной, но в дальнейшем может уступить более устойчивой архитектуре.

Примером более устойчивой архитектуры могут послужить кубиты на основе холодных атомов. В ближайшее время можно ожидать публикации с демонстрацией рекордной степени точности двухкубитного гейта, построенного на основе подхода с наносекундным временным масштабом. Совершенствование и масштабирование данной технологии может привести к появлению программируемого атомного вычислителя с рекордным количеством кубитов.

Наиболее перспективными на дальнем временном горизонте остаются вычислители на основе оптических схем. Исследования последних лет в значительной мере конкретизировали понимание того, как должен быть устроен оптический вычислитель большого масштаба с коррекцией ошибок. То есть устройство, полностью выводящее отрасль квантовых вычислений из эпохи NISQ. Можно со значительной степенью уверенности утверждать, что это будет система с кубитами на основе сжатых состояний с непрерывными переменными. Главными ограничениями для такого вычислителя остаётся неизбежное возникновение ошибки телепортационного гейта из-за невозможности сжать квадратуру квантового состояния до нуля, а также потери излучения в волокне. Существенными шагами в направлении к созданию масштабируемого оптического вычислителя станет экспериментальная демонстрация устойчивой коррекции ошибки и исполнение вычислителя такого типа в виде интегрально-оптической схемы.  

Облачные квантово-вычислительные сервисы могут начать внедряться в программные продукты для решения задач оптимизации при помощи вариационных алгоритмов уже в обозримом будущем, на горизонте 5-7 лет. Наиболее вероятно, что аппаратным обеспечением данных сервисов будут оставаться вычислители на основе сверхпроводящих схем или холодных атомов. Значительное развитие может получить инфраструктура квантовой оптической связи, призванная, в первую очередь, решать задачи обеспечения информационной безопасности. Можно ожидать, что со временем данные сети будут усложняться, переходя на обмен состояниями более высокой размерности и обеспечивая реализацию коррекции ошибок за счёт простых интегрально-оптических устройств.

В отдалённой перспективе, на горизонте 15 и более лет, это может привести к созданию разветвлённой квантово-коммуникационной сети, объединяющей, в том числе, оптические квантовые компьютеры, что позволит использовать квантово-вычислительные ресурсы более широко и эффективно.